Fórmula para calcular a diagonal de um losango

Um losango é um quadrilátero com quatro lados iguais, um quadrilátero com duas diagonais perpendiculares entre si no ponto médio de cada linha é um losango, um paralelogramo com dois lados adjacentes iguais... Além de quadrados, retângulos, triângulos... o losango é uma das formas importantes na matemática e na vida.

Além da fórmula para calcular o perímetro e a área de um losango , a maneira de calcular a diagonal de um losango - a linha que conecta os vértices opostos do losango - também é muito importante.

O artigo abaixo ajudará você a aprender como calcular a diagonal de um losango com exemplos específicos. Consulte-o.

Índice

• Diagonal de um losango
• Propriedades das diagonais de um losango
• Fórmula para calcular a diagonal de um losango
• Problema de cálculo da diagonal do losango

Diagonal de um losango

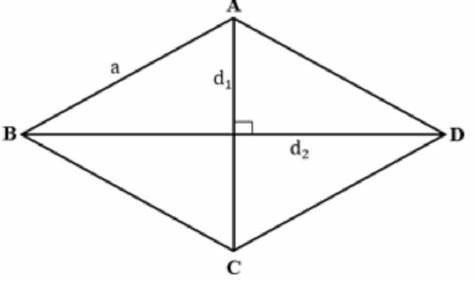
• A diagonal de um losango é a linha que conecta dois vértices opostos do losango.
• Um losango tem duas diagonais que se cruzam no ponto médio do losango.
• A diagonal divide o losango em dois triângulos equiláteros com lados iguais.

Propriedades das diagonais de um losango

As duas diagonais em um losango têm as seguintes propriedades:

• Duas diagonais iguais: As duas diagonais de um losango têm o mesmo comprimento.
• O ângulo entre duas diagonais é um ângulo reto: as duas diagonais de um losango se cruzam no ponto médio do losango e formam um ângulo reto.
• As diagonais são os eixos de simetria de um losango: Cada diagonal de um losango é um eixo de simetria do losango, dividindo o losango em duas metades simétricas.
• Diagonais são diagonais de dois triângulos equiláteros: Cada diagonal de um losango é uma diagonal de dois triângulos equiláteros, formados por lados iguais.
• O produto dos comprimentos das duas diagonais é igual ao produto dos comprimentos dos dois lados de um losango: O produto dos comprimentos das duas diagonais é igual ao produto dos comprimentos dos dois lados de um losango. Ou seja, se denotarmos a diagonal por d, e os lados por a e b, temos d² = a² + b².

Essas propriedades são características dos losangos e são usadas em muitos problemas geométricos que envolvem losangos.

Fórmula para calcular a diagonal de um losango

Considere o exemplo abaixo para derivar a fórmula para calcular a diagonal de um losango.

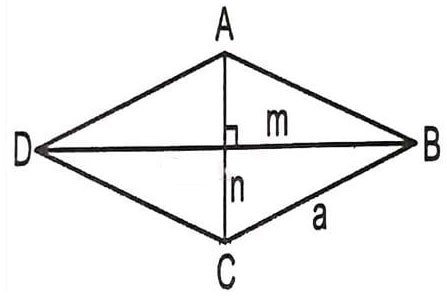
Suponha que precisamos calcular o comprimento da diagonal de um losango ABCD com lado a e um ângulo ABC = 60 graus -> qual é a fórmula para calcular a diagonal de um losango neste caso?

Solução:

Como ABCD é um losango, todos os lados são iguais a a.

Considere o triângulo ABC com: AB = BC = a

Novamente: ABC = 60 graus => O triângulo ABC é um triângulo equilátero de lado a.

=> AB = AC = BC = a

=> O comprimento da diagonal do losango é AC = BD = a.

A solução acima é uma das fórmulas mais simples e fáceis de entender para calcular a diagonal de um losango.

Fórmula para calcular a diagonal de um losango conhecendo a área e a diagonal restante

Da fórmula para calcular a área de um losango:

S = (axb) : 2

Temos a fórmula para o comprimento diagonal da seguinte forma:

a = S x 2 : b

ou

b = S x 2 : a

Lá dentro:

• S é a área
• a e b são os comprimentos das duas diagonais

Use as propriedades geométricas de um losango para calcular o comprimento da diagonal sem usar o teorema de Pitágoras. Especificamente:

A diagonal de um losango é a média das duas alturas.

Diagonal = raiz quadrada de (altura longa + altura curta)²

A diagonal de um losango é metade do perímetro do losango.

Diagonal = 1/2 x perímetro do losango.

Problema de cálculo da diagonal do losango

Problema 1: Dado um losango com área de 360 ​​centímetros quadrados e comprimento diagonal de 24 centímetros. Calcule o comprimento da segunda diagonal

Solução:

De acordo com a fórmula da área de um losango: axb : 2

Temos a segunda diagonal: 360 x 2 : 24 = 30cm

Resposta: 30cm

Problema 2:

Um losango tem uma área de 4dm, o comprimento de uma diagonal é 3/5 dm. Calcule o comprimento da segunda diagonal. Solução:

O comprimento da segunda diagonal é:

(4 x 2) : 3/5 = 40/3 (dm)

Lição 3: As duas diagonais de um losango têm comprimentos de 160 cm e 120 cm. Calcule a altura do losango, sabendo que a razão entre a altura e o comprimento do lado do losango é 24:25.

Solução:

A área do losango é: 160,120:2 = 9 600 (cm2).

Como a razão entre a altura e o comprimento do lado de um losango é 24:25, podemos considerar que a altura do losango é 24a e o lado do losango é 25a.

Temos então a área do losango: 25a.24a = 9 600 a2 = 16 a = 4 cm.

A altura do losango é: 24,4 = 96 (cm).

Então a altura do losango é 96 cm.

Lição 4: 

Dado o losango ABCD com comprimento de lado 12,5 cm, altura 6,72 cm e AC é menor que BD. Quais são os comprimentos das diagonais AC e BD respectivamente?

Prêmio:

Aplique a fórmula para calcular a área de um losango: S = ha = 6,72 x 12,5 = 84cm.
=> 1/2 CA x BD = 84 => 2CA.BD = 336

Seja O a intersecção das duas diagonais de um losango.

Temos AOB é um triângulo retângulo em O então AB2 = OA2 + OB2

Em que, OA = 1/2 AC, OB = 1/2 BD

=> 12,52 = 1/4 (AC2 + BD2) <=> 625 = AC2 + BD2

AC2 + BD2 = 625 <=> AC2 + BD2+ 2AC.BD = 625 + 336 <=> (AC + BD)2 = 961 <=> AC + BD = 31 (1)

AC2 + BD2 = 625 <=> AC2 + BD2- AC.BD = 625 -336 <=> (BD - AC)2 = 289 <=> BD - AC = 17 (De acordo com o problema BD > AC) (2)

De (1) e (2), temos:

BD = 24, CA = 7 cm.

Lição 5: 

O losango ABCD tem lados iguais a 10 unidades. Calcule o comprimento da diagonal do losango.

Solução: O comprimento da diagonal do losango ABCD é:

Diagonal = raiz quadrada de 2(10²) = raiz quadrada de 200 = 14,14 unidades de comprimento.

Portanto, o comprimento da diagonal do losango ABCD é 14,14 unidades de comprimento.

Lição 6:

O losango ABCD tem uma diagonal de 12 unidades. Calcule o perímetro do losango.

Solução: Como um losango tem quatro lados iguais, seu perímetro será a soma dos comprimentos dos quatro lados, ou seja:

Perímetro = 4 x comprimento lateral = 4 x 6 = 24 unidades de comprimento.

Portanto, o perímetro do losango ABCD é de 24 unidades de comprimento.