é o ângulo entre o eixo OI e (P)
Como recuperar o acesso ao disco rígido, corrigir o erro de não conseguir abrir o disco rígido
Neste artigo, mostraremos como recuperar o acesso ao seu disco rígido em caso de falha. Vamos acompanhar!
Área do cilindro: Área da superfície do cilindro, área total do cilindro
Vamos aprender a fórmula para calcular a área lateral, área total e altura de um cilindro para aplicar nos estudos e no dia a dia.
Índice
- Como calcular a área de um cilindro
- Calcular a altura do cilindro
- Fórmula para calcular o raio da base de um cilindro
- O que é um cilindro circular?
- Fórmula para calcular a área da seção transversal de um cilindro
- Exemplo de cálculo da área de um cilindro
Como calcular a área de um cilindro
A área de um cilindro inclui a área lateral e a área total.
Você pode inserir a altura e o raio do cilindro na tabela abaixo para saber a área lateral e a área total do cilindro.
Fórmula para calcular a área lateral de um cilindro
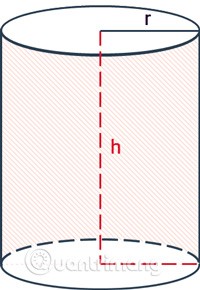
A área lateral de um cilindro inclui apenas a área da superfície que envolve o cilindro, não incluindo a área das duas bases.
A fórmula para calcular a área lateral de um cilindro é a circunferência do círculo da base multiplicada pela altura.
 |
Lá dentro:
|
Exemplo: 1
Um cilindro circular tem raio da base r = 5 cm e altura h = 7 cm. Calcular a área lateral de um cilindro vertical.
Solução: Área da superfície de um cilindro circular: Sxq = 2.π.rh = 2π.5.7 = 70π = 219.8 (cm2).
Exemplo: 2
Dado o quadrado ABCD com lado 2a. Sejam O e O' os pontos médios dos lados AB e CD, respectivamente. Ao girar esse quadrado em torno do eixo OO', obtemos um cilindro giratório. Calcule a área da superfície do cilindro rotativo.
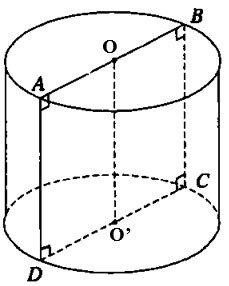
Solução:
O raio do círculo base é r= CD= a
A altura do cilindro é h= OO'= AD=2a
Portanto a área lateral do cilindro é Sxq = 2πrh = 2π.a.2a =4a2π
Fórmula para calcular a área total de um cilindro
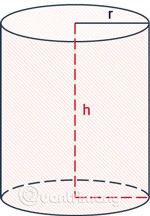
A área total é calculada como a magnitude de todo o espaço ocupado pela figura, incluindo a área lateral e a área das duas bases circulares.
A fórmula para calcular a área total de um cilindro é a área lateral mais a área das duas bases.
 |
|
Exemplo 1 : Calcule a área total de um cilindro com base 3 e altura 5.
Solução:
A área total é Stp = Sxq + 2Sd = 2πr(r+h) = 2π.3(3+5) = 48π
Calcular a altura do cilindro
A altura de um cilindro é a distância entre as duas bases do cilindro.
Calcular a altura de um cilindro sabendo a área total e o raio da base
Por exemplo: Dado um cilindro com raio da base R = 8 cm e área total 564π cm2 . Calcule a altura do cilindro.
Prêmio:
Nós temos
Calcular a altura de um cilindro sabendo a área lateral
=>
Fórmula para calcular o raio da base de um cilindro
1. Fórmula para calcular a circunferência de um círculo; área do círculo
O círculo tem circunferência C=2πr
=>
O círculo com base tem área S=πr2
=>
Por exemplo. Calcule o raio da base do cilindro nos seguintes casos:
um. A circunferência do círculo base é 6π
b. A área da base é 25π
Solução:
um. O raio do círculo base é
b. O raio do círculo base é
2. A base é o círculo inscrito no polígono
- Inscrito em qualquer triângulo: sendo S a área do triângulo e p o semiperímetro
- Inscrito em um triângulo equilátero: lado
- Quadrado inscrito:
Exemplo 1 . Dado um cilindro inscrito em um cubo de aresta a. Calcule o raio desse cilindro.
O raio do cilindro é:
Exemplo 2 . Dado um prisma regular ABC.A'B'C' com , o volume circunscrito ao redor do cilindro. Calcule o raio desse cilindro.
O volume do prisma é
A base de um prisma regular é um triângulo equilátero, então => o lado
Portanto, o raio da base do cilindro é:
3. A base é o círculo que circunscreve o polígono.
Circunscrito em qualquer triângulo:
Lá dentro:
- a, b, c são os comprimentos dos três lados do triângulo
- p é o semiperímetro do triângulo:
Circunferência de um triângulo retângulo: hipotenusa
Periferia do triângulo equilátero: lado
Circunferência do quadrado: lado
Por exemplo:
Calcule o raio da base do cilindro que circunscreve a pirâmide regular S.ABC nos seguintes casos:
um. ABC é um triângulo retângulo em A com AB = a e AC = a√3
b. ABC tem AB= 5; CA= 7; BC=8
Prêmio:
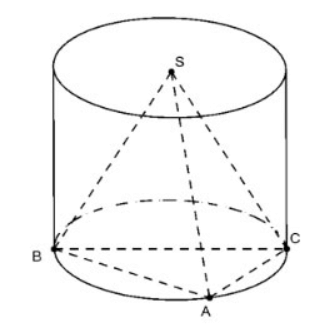
um. Hipotenusa
Como ABC é um ângulo reto em A, raio R = 0,5.BC = a
b. O semiperímetro do triângulo ABC é
O que é um cilindro circular?
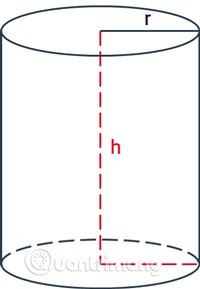
Um cilindro circular é um cilindro com duas bases circulares iguais e paralelas entre si.
Cilindros são usados com bastante frequência em problemas de geometria, dos mais básicos aos mais complexos, nos quais a fórmula para calcular a área e o volume dos cilindros costuma ser usada de forma diferente. Se você já sabe como calcular a área e a circunferência de um círculo, pode facilmente deduzir as fórmulas para calcular o volume, a área lateral e a área total de um cilindro.
 |
 |
Fórmula para calcular a área da seção transversal de um cilindro
Cortar o cilindro com o plano (P) através do eixo
- A seção transversal resultante é um retângulo.
 |
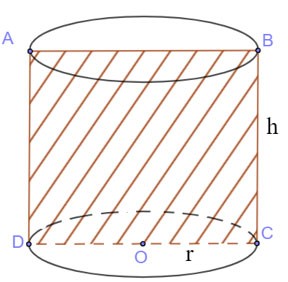Área da seção transversal: SABCD = BC.CD =2r.h |
Cortar o cilindro pelo plano (P) paralelo e a uma distância x do eixo
 |
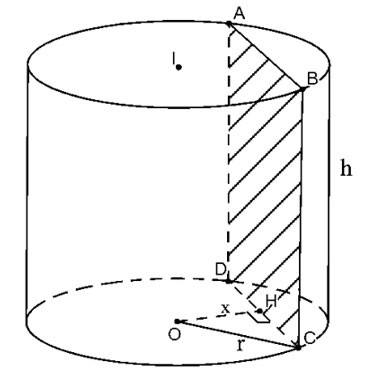A seção transversal resultante é o retângulo ABCD, como mostrado acima. Seja H o ponto médio de CD, temos OH ⊥ CD=>
Portanto, a área da secção transversal
|
Cortar o cilindro com um plano (P) não perpendicular ao eixo, mas cortar todas as geratriz do cilindro
 |
A seção transversal formada é um círculo de centro O' e raio O'A'=r Área da seção transversal: S= πr2 |
Corte o cilindro pelo plano (P) não perpendicular ao eixo, mas corte todas as geratrizes do cilindro.
 |
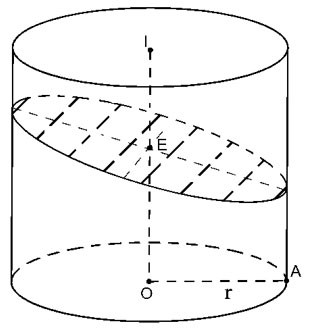A seção transversal resultante é uma elipse (E) com eixo menor 2r => a=r Eixo grande é igual a com Portanto, área S= π. ab= |
Exemplo de cálculo da área de um cilindro
Lição 1 :
A área lateral de um cilindro tem uma circunferência de base circular de 13cm e uma altura de 3cm.
Prêmio:
Temos: circunferência do círculo C = 2R.π = 13cm, h = 3cm
Portanto a área lateral do cilindro é:
Sxq = 2πr.h = Ch = 13,3 = 39 (cm²)
Lição 2 : Dado um cilindro com um raio de círculo de base de 6 cm, enquanto a altura da base até o topo do cilindro tem 8 cm de espessura. Qual é a área lateral e a área total do cilindro?
Prêmio
De acordo com a fórmula, temos o semicírculo da base r = 6 cm e a altura do cilindro h = 8 cm. Portanto, temos a fórmula para calcular a área lateral de um cilindro e a área total de um cilindro da seguinte forma:
Área da superfície do cilindro = 2 x π xrxh = 2 x π x 6 x 8 = ~ 301 cm²
Área total do cilindro = 2 Π x R x (R + H) = 2 X π x 6 x (6 + 8) = ~ 527 cm²
Lição 3 : Um cilindro tem raio de base de 7cm e área lateral de 352cm2.
Então, a altura do cilindro é:
(A) 3,2 cm; (B) 4,6 cm; (C) 1,8 cm
(D) 2,1 cm; (E) Outro resultado
Selecione o resultado correto.
Solução: Temos
Então, a resposta E está correta.
Lição 4 : A altura de um cilindro é igual ao raio do círculo da base. A área lateral do cilindro é 314 cm2. Calcule o raio do círculo da base e o volume do cilindro (arredondar o resultado para duas casas decimais).
Prêmio:
A área lateral do cilindro é 314cm2
Temos Sxq = 2.π.rh = 314
Onde r = h
Então 2πr² = 314 => r² ≈ 50 => r ≈ 7,07 (cm)
Volume do cilindro: V = π.r2.h = π.r3 ≈ 1109,65 (cm³).
Esperamos que o artigo acima tenha ajudado você a compreender conhecimentos básicos e avançados sobre cilindros, como calcular a área total e a área lateral de um cilindro.
Como usar o recurso de Conscientização de Conversação e Escuta ao Vivo nos AirPods
À primeira vista, os AirPods parecem fones de ouvido sem fio comuns. Mas tudo mudou quando alguns recursos pouco conhecidos foram descobertos.
Tudo sobre o iOS 26
A Apple apresentou o iOS 26 – uma grande atualização com um novo design de vidro fosco, experiências mais inteligentes e melhorias em aplicativos familiares.
Os melhores laptops para estudantes em 2025
Os alunos precisam de um tipo específico de laptop para seus estudos. Ele não deve apenas ser potente o suficiente para um bom desempenho na área de estudo escolhida, mas também compacto e leve o suficiente para ser carregado o dia todo.
Como adicionar uma impressora ao Windows 10
Adicionar uma impressora ao Windows 10 é simples, embora o processo para dispositivos com fio seja diferente do que para dispositivos sem fio.
Como verificar a RAM e verificar erros de RAM no seu computador com a maior taxa de precisão
Como você sabe, a RAM é um componente de hardware muito importante em um computador, atuando como memória para processar dados e é o fator que determina a velocidade de um laptop ou PC. No artigo abaixo, o WebTech360 apresentará algumas maneiras de verificar erros de RAM usando software no Windows.
Diferença entre TV comum e Smart TV
As Smart TVs realmente conquistaram o mundo. Com tantos recursos excelentes e conectividade à Internet, a tecnologia mudou a maneira como assistimos TV.
Por que o freezer não tem luz, mas a geladeira tem?
Geladeiras são eletrodomésticos comuns em residências. As geladeiras geralmente têm 2 compartimentos, o compartimento frio é espaçoso e tem uma luz que acende automaticamente toda vez que o usuário o abre, enquanto o compartimento do freezer é estreito e não tem luz.
2 maneiras de corrigir o congestionamento da rede que deixa o Wi-Fi lento
As redes Wi-Fi são afetadas por muitos fatores além de roteadores, largura de banda e interferência, mas existem algumas maneiras inteligentes de melhorar sua rede.
Como fazer downgrade do iOS 17 para o iOS 16 sem perder dados usando o Tenorshare Reiboot
Se você quiser voltar para o iOS 16 estável no seu telefone, aqui está o guia básico para desinstalar o iOS 17 e fazer o downgrade do iOS 17 para o 16.
O que acontece com o corpo quando você come iogurte todos os dias?
Iogurte é um alimento maravilhoso. É bom comer iogurte todos os dias? Quando você come iogurte todos os dias, como seu corpo muda? Vamos descobrir juntos!
Que tipo de arroz é melhor para a saúde?
Este artigo discute os tipos de arroz mais nutritivos e como maximizar os benefícios para a saúde de qualquer arroz que você escolher.
Como acordar na hora certa pela manhã
Estabelecer um horário de sono e uma rotina para dormir, mudar o despertador e ajustar a dieta são algumas das medidas que podem ajudar você a dormir melhor e acordar na hora certa pela manhã.
Dicas para jogar Rent Please! Simulador de Proprietário para Iniciantes
Alugue, por favor! Landlord Sim é um jogo de simulação para dispositivos móveis para iOS e Android. Você jogará como proprietário de um complexo de apartamentos e começará a alugar um apartamento com o objetivo de reformar o interior do seu apartamento e deixá-lo pronto para inquilinos.
Últimos códigos de defesa de torre de banheiro e como inseri-los
Obtenha o código do jogo Bathroom Tower Defense Roblox e resgate recompensas emocionantes. Elas ajudarão você a melhorar ou desbloquear torres com maior dano.