Como recuperar o acesso ao disco rígido, corrigir o erro de não conseguir abrir o disco rígido
Neste artigo, mostraremos como recuperar o acesso ao seu disco rígido em caso de falha. Vamos acompanhar!
Fórmula para calcular a área de um paralelogramo, o perímetro de um paralelogramo
A fórmula para calcular a área e o perímetro de um paralelogramo é um conhecimento básico. Consulte a fórmula que o Quantrimang.com compilou abaixo.
Índice
- 1. Área do paralelogramo
- 2. Perímetro do paralelogramo
- 3. O que é um paralelogramo?
- 4. Questões de múltipla escolha para revisar paralelogramos
- 5. Exemplos de cálculo de perímetro e área de paralelogramo
1. Área do paralelogramo
A área de um paralelogramo é medida pelo tamanho da superfície, que é a parte plana visível do paralelogramo.
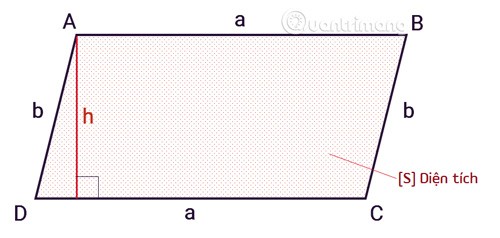
A área de um paralelogramo é calculada pela fórmula igual ao produto da base pela altura.
SABCD = axh
Lá dentro:
Sé a área de um paralelogramo.aé a base do paralelogramo.hé a altura, do topo à base, de um paralelogramo.
2. Perímetro do paralelogramo
O perímetro de um paralelogramo é calculado somando o comprimento das linhas que circundam a forma, que também é a linha que circunda toda a área, igual a 2 vezes a soma de qualquer par de lados adjacentes.
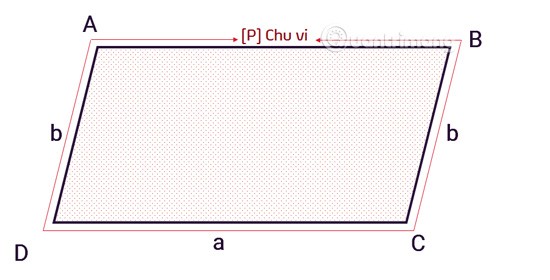
Em outras palavras, o perímetro de um paralelogramo é a soma dos comprimentos dos quatro lados. A fórmula específica é a seguinte:
C = 2 x (a+b)
Lá dentro:
Cé o perímetro de um paralelogramo.aebsão lados adjacentes de um paralelogramo.
3. O que é um paralelogramo?
Definir
Um paralelogramo é um quadrilátero com 2 pares de lados paralelos ou 1 par de lados paralelos e iguais. Um paralelogramo tem dois ângulos opostos iguais e duas diagonais que se cruzam no ponto médio da forma.
O paralelogramo pode ser considerado um caso especial de trapézio.
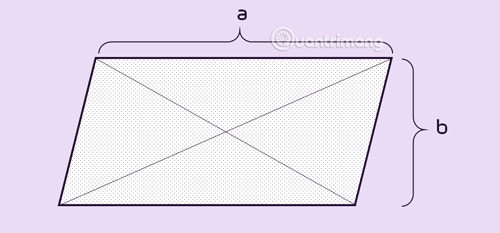
Propriedades do paralelogramo
Em paralelogramo:
- Lados opostos são iguais.
- Ângulos opostos são iguais.
- Duas diagonais se cruzam no ponto médio de cada linha.
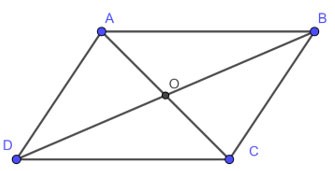
ABCD é um paralelogramo, AC intercepta BD em O. Então:
• AB = CD, AD = BC
•
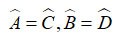
• OA = OC, OB = OD
Sinais de reconhecimento
a) Um quadrilátero com lados opostos paralelos é um paralelogramo.
b) Um quadrilátero com lados opostos iguais é um paralelogramo.
c) Um quadrilátero com dois lados opostos paralelos e iguais é um paralelogramo.
d) Um quadrilátero com ângulos opostos iguais entre si é um paralelogramo.
e) Um quadrilátero com duas diagonais que se cruzam no ponto médio de cada uma é um paralelogramo.
4. Questões de múltipla escolha para revisar paralelogramos
Exercício 1 : Escolha a frase errada.
A. Um paralelogramo tem duas diagonais que se cruzam no ponto médio de cada diagonal.
B. O paralelogramo tem dois ângulos opostos iguais
C. Um paralelogramo tem duas diagonais perpendiculares entre si.
D. Dois paralelogramos têm dois pares de lados opostos paralelos.
Solução
Em paralelogramo:
+ Paralelogramo tem lados opostos paralelos
+ Lados opostos são iguais
+ Duas diagonais se cruzam no ponto médio de cada linha, então C está incorreto.
A resposta correta é: C
Exercício 2 : Dado o paralelogramo ABCD com  = α > 900. Fora do paralelogramo, desenhe os triângulos equiláteros ADE, ABF. Que tipo de triângulo é o triângulo CEF? Escolha a melhor resposta
A. Triângulo
B. Triângulo isósceles
C. Triângulo equilátero
D. Triângulo obtusângulo
Responder:
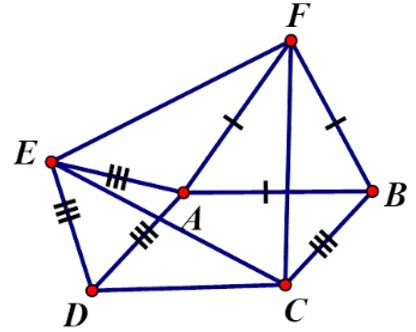
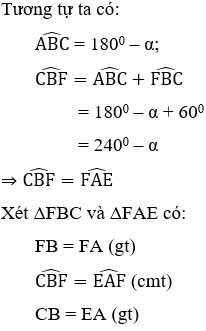
⇒ ΔFBC = ΔFAE (cgc) ⇒ CF = FE (2)
De (1) e (2) podemos deduzir que CF = FE = EC, então o triângulo CEF é equilátero.
Lição 3 : Escolha a frase errada. ABCD é um paralelogramo. Então:
A. AB = CD
B. d.C. = a.C.
C. Teste do paralelogramo com respostas
D. AC = BD
Solução
Em paralelogramo:
+ Paralelogramo tem lados opostos paralelos
+ Lados opostos são iguais
+ Duas diagonais se cruzam no ponto médio de cada linha, então D está incorreto.
Lição 4 : Preencha a lacuna com a frase apropriada: “Um quadrilátero com duas diagonais… é um paralelogramo.”
A. igual
B. interseccionar
C. se cruzam no ponto médio de cada linha
D. paralelo
Solução
Sinais:
Um quadrilátero com duas diagonais que se cruzam no ponto médio de cada uma é um paralelogramo.
Lição 5 : Escolha a frase errada:
A. Um quadrilátero com dois pares de lados opostos paralelos é um paralelogramo.
B. Um trapézio com dois ângulos iguais adjacentes a uma base é um paralelogramo.
C. Um quadrilátero com dois pares de lados opostos iguais é um paralelogramo.
D. Um quadrilátero com dois pares de ângulos opostos iguais é um paralelogramo.
Solução
Sinais:
+ Um quadrilátero com lados opostos paralelos é um paralelogramo, então A está correta.
+ Um quadrilátero com lados opostos iguais é um paralelogramo, então D está correto.
+ Um quadrilátero com ângulos opostos iguais entre si é um paralelogramo, então D está correto.
Percebendo que um trapézio com dois ângulos iguais adjacentes a uma base é um trapézio isósceles, então B está incorreto.
A resposta correta é: B
5. Exemplos de cálculo de perímetro e área de paralelogramo
Exemplo 1 : Dado um paralelogramo com uma base de 12 cm, um lado de 7 cm e uma altura de 5 cm. Calcule o perímetro e a área desse paralelogramo?
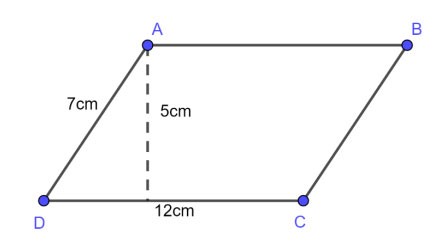
Prêmio:
O perímetro do paralelogramo é:
P = 2 x (12 + 7) = 38 (cm)
A área de um paralelogramo é:
S = axh = 12 x 5 = 60 (cm2)
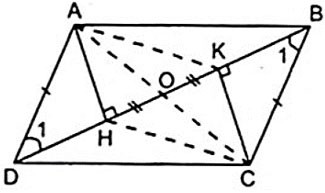
Exemplo 2:
Dado o paralelogramo ABCD com H e K sendo os pés das altitudes traçadas dos vértices A, C e BD, respectivamente.
a) Prove que AHCK é um paralelogramo.
b) Seja O o ponto médio de HK. Prove que A, O, C são colineares.
Instruir:
a) Da hipótese temos:
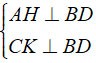⇒ AH//CK. ( 1 )
Aplicando propriedades dos lados dos paralelogramos e propriedades dos ângulos alternos, temos:
⇒ Δ ADH = Δ CBK
(hipotenusa – caso de ângulo agudo)
⇒ AH = CK (lados correspondentes são iguais) ( 2 )
De (1) e (2) temos o quadrilátero AHCK com lados opostos paralelos e iguais é um paralelogramo.
b) Aplicar as propriedades das diagonais do paralelogramo AHCK
O paralelogramo AHCK tem duas diagonais AC e HK que se cruzam no ponto médio de cada reta. Como O é o ponto médio de HK, O também é o ponto médio de AC.
⇒ A, O, C estão em uma linha reta.
Além dos paralelogramos, as fórmulas para calcular a área e o perímetro de outras formas geométricas comuns, como losangos , quadrados , trapézios , retângulos ... também são muito importantes e amplamente aplicadas no estudo e na vida.
Espero que, com o artigo acima, você tenha entendido e compreendido melhor o conhecimento básico sobre paralelogramos. Deixe um comentário abaixo se tiver alguma dúvida ou comentário para discutir com o Quantrimang.com.
Como usar o recurso de Conscientização de Conversação e Escuta ao Vivo nos AirPods
À primeira vista, os AirPods parecem fones de ouvido sem fio comuns. Mas tudo mudou quando alguns recursos pouco conhecidos foram descobertos.
Tudo sobre o iOS 26
A Apple apresentou o iOS 26 – uma grande atualização com um novo design de vidro fosco, experiências mais inteligentes e melhorias em aplicativos familiares.
Os melhores laptops para estudantes em 2025
Os alunos precisam de um tipo específico de laptop para seus estudos. Ele não deve apenas ser potente o suficiente para um bom desempenho na área de estudo escolhida, mas também compacto e leve o suficiente para ser carregado o dia todo.
Como adicionar uma impressora ao Windows 10
Adicionar uma impressora ao Windows 10 é simples, embora o processo para dispositivos com fio seja diferente do que para dispositivos sem fio.
Como verificar a RAM e verificar erros de RAM no seu computador com a maior taxa de precisão
Como você sabe, a RAM é um componente de hardware muito importante em um computador, atuando como memória para processar dados e é o fator que determina a velocidade de um laptop ou PC. No artigo abaixo, o WebTech360 apresentará algumas maneiras de verificar erros de RAM usando software no Windows.
Diferença entre TV comum e Smart TV
As Smart TVs realmente conquistaram o mundo. Com tantos recursos excelentes e conectividade à Internet, a tecnologia mudou a maneira como assistimos TV.
Por que o freezer não tem luz, mas a geladeira tem?
Geladeiras são eletrodomésticos comuns em residências. As geladeiras geralmente têm 2 compartimentos, o compartimento frio é espaçoso e tem uma luz que acende automaticamente toda vez que o usuário o abre, enquanto o compartimento do freezer é estreito e não tem luz.
2 maneiras de corrigir o congestionamento da rede que deixa o Wi-Fi lento
As redes Wi-Fi são afetadas por muitos fatores além de roteadores, largura de banda e interferência, mas existem algumas maneiras inteligentes de melhorar sua rede.
Como fazer downgrade do iOS 17 para o iOS 16 sem perder dados usando o Tenorshare Reiboot
Se você quiser voltar para o iOS 16 estável no seu telefone, aqui está o guia básico para desinstalar o iOS 17 e fazer o downgrade do iOS 17 para o 16.
O que acontece com o corpo quando você come iogurte todos os dias?
Iogurte é um alimento maravilhoso. É bom comer iogurte todos os dias? Quando você come iogurte todos os dias, como seu corpo muda? Vamos descobrir juntos!
Que tipo de arroz é melhor para a saúde?
Este artigo discute os tipos de arroz mais nutritivos e como maximizar os benefícios para a saúde de qualquer arroz que você escolher.
Como acordar na hora certa pela manhã
Estabelecer um horário de sono e uma rotina para dormir, mudar o despertador e ajustar a dieta são algumas das medidas que podem ajudar você a dormir melhor e acordar na hora certa pela manhã.
Dicas para jogar Rent Please! Simulador de Proprietário para Iniciantes
Alugue, por favor! Landlord Sim é um jogo de simulação para dispositivos móveis para iOS e Android. Você jogará como proprietário de um complexo de apartamentos e começará a alugar um apartamento com o objetivo de reformar o interior do seu apartamento e deixá-lo pronto para inquilinos.
Últimos códigos de defesa de torre de banheiro e como inseri-los
Obtenha o código do jogo Bathroom Tower Defense Roblox e resgate recompensas emocionantes. Elas ajudarão você a melhorar ou desbloquear torres com maior dano.