Fórmula para calcular altura em triângulos regulares, isósceles, equiláteros e retângulos

A altitude em um triângulo é uma linha reta com propriedades importantes e está intimamente relacionada a problemas de geometria plana. Então, qual é a altura? Como calcular a altura de um triângulo? Consulte o artigo abaixo para obter a resposta e a fórmula mais simples para calcular a altura de um triângulo.

Índice

• Fórmula para calcular a altura de um triângulo
  • Calcular a altura de um triângulo regular
  • Calcular a altura em um triângulo equilátero
  • Fórmula para calcular a altura em um triângulo retângulo
  • Fórmula para calcular a altura em um triângulo isósceles
• Definição de altitude em um triângulo
• Propriedades das três alturas de um triângulo

Fórmula para calcular a altura de um triângulo

Calcular a altura de um triângulo regular

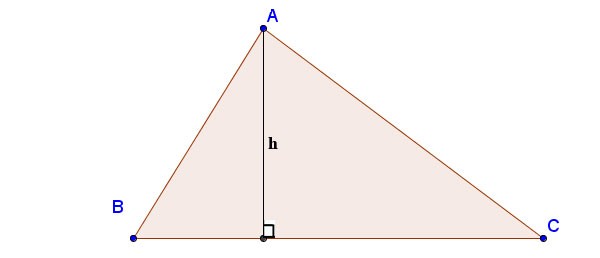
Como calcular a altura de um triângulo usando a fórmula de Heron:

Com a, b, c sendo os comprimentos dos lados; ha é a altitude traçada do vértice A ao lado BC; p é o semiperímetro:

Por exemplo: 

Dado o triângulo ABC, lado AB = 4 cm, lado BC = 7 cm, lado AC = 5 cm. Calcule a altitude AH de A que intercepta BC em H e calcule a área de ABC.

Prêmio:

Meio perímetro do triângulo: P = (AB + BC + AC) : 2 = (4 + 7 + 5) : 2 = 8(cm)

Altura   

=>

Considere o triângulo ABC, temos:

Então,

Calcular a altura em um triângulo equilátero

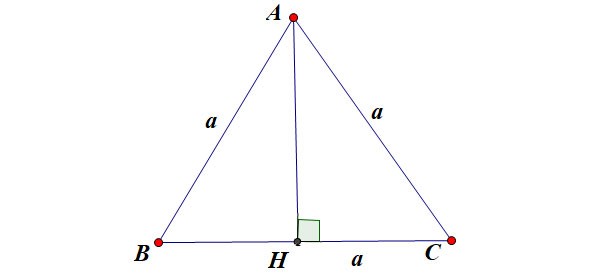
Suponha que o triângulo equilátero ABC tenha lado de comprimento a, conforme mostrado na figura:

Lá dentro:

• h é a altura de um triângulo equilátero
• a é o comprimento do lado de um triângulo equilátero

Fórmula para calcular a altura em um triângulo retângulo

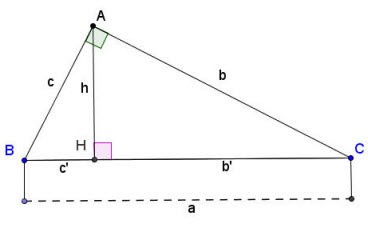
Suponha que haja um triângulo retângulo ABC diretamente em A, como mostrado acima:

Fórmula para calcular lados e alturas em um triângulo retângulo:

1. a2 = b2 + c2

2. b2 = ab′ e c2 = ac′

3. ah = bc

4. h2 = b′.c'

5.

Lá dentro:

• a, b, c são os lados de um triângulo retângulo como mostrado acima;
• b' é a projeção da aresta b sobre a hipotenusa;
• c' é a projeção da aresta c sobre a hipotenusa;
• h é a altura de um triângulo retângulo desenhado a partir do vértice do ângulo reto A até a hipotenusa BC.

Exemplo 1: Dado o triângulo ABC retângulo em A, altura AH. Calcule BC, AC, AH sabendo que AB = 15 cm, HC = 16 cm.

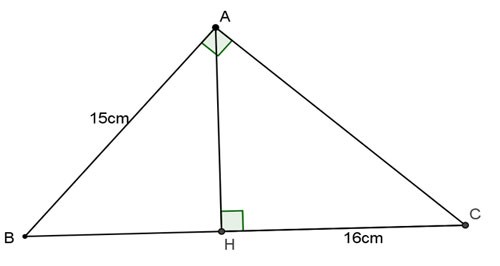
Prêmio:

Aplicando a fórmula algébrica no triângulo retângulo ABC temos:

AC2 = CH.BC = 16.BC

De acordo com o teorema de Pitágoras para o triângulo retângulo ABC com ângulo reto A, temos:

AB2 + AC2 = BC2

⇔ 152 + 16.BC = BC2

⇔ BC2 - 16.BC - 225 = 0

⇔ BC2 - 25.BC + 9.BC - 225 = 0

⇔ BC(BC - 25) + 9(BC - 25) = 0

⇔ (BC - 25)(BC + 9) = 0

⇔ BC = 25 ou BC = -9 (eliminar)

⇒ AC2 = 16.BC = 16,25 = 400 ⇒ AC = 20 (cm)

Considere o triângulo retângulo ABC com: AH.BC = AB.AC (fórmula geométrica)

=> AH = AB.AC/BC = 15,20/25 = 12(cm)

Então BC=25(cm); CA=20(cm); AH=12(cm)

Exemplo 2 :

O triângulo ABC é retângulo em A, AB=24cm, AC=32cm. A bissetriz perpendicular de BC intercepta AC, BC em D e E respectivamente. Calcular DE.

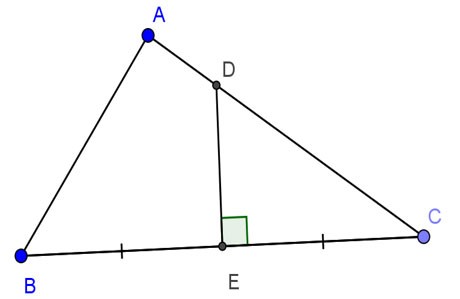
Prêmio:

Considerando o triângulo retângulo ABC, temos:

BC2 = AB2 + AC2 (de acordo com o teorema de Pitágoras)

BC2 = 242+ 322

BC2 = 1600

BC = 40(cm)

CE = BC : 2 = 40 : 2 = 20(cm)

Considere o triângulo retângulo ACB e o triângulo retângulo ECD com:

Existe ∠A = ∠E = 90o

∠C comum

=> Triângulo ACB ∾ triângulo ECD (gg)

=> CA/CE = AB/ED

=> ED = AB.EC/AC = 15cm

Então ED = 15cm

Fórmula para calcular a altura em um triângulo isósceles

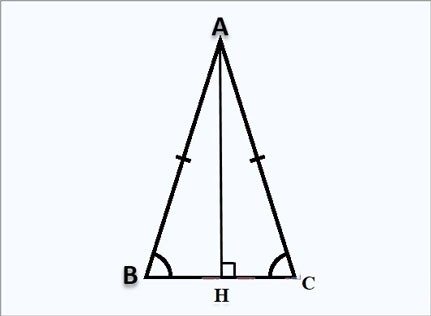
Suponha que você tenha um triângulo isósceles ABC em A, a altura AH é perpendicular em H, conforme mostrado acima:

Fórmula para calcular a altura AH:

Como o triângulo ABC é isósceles em A, a altura AH também é a mediana, então:

⇒ HB=HC= ½BC

Aplicando o teorema de Pitágoras no triângulo retângulo ABH à direita em H, temos:

AH² + BH² = AB²

⇒AH²=AB²−BH²

Por exemplo : Dado que Δ ABC está equilibrado em A com BC = 30(cm), altura AH = 20(cm). Calcule a altura correspondente ao lado desse triângulo isósceles.

Solução: Considere Δ ABC isósceles em A com BC = 30(cm)

⇒ BH = CH = 15(cm).

Aplicando o teorema de Pitágoras temos:

Agora temos que calcular BK = ?

Nós temos:

Por outro lado

Portanto, temos ⇔

Definição de altitude em um triângulo

Uma altitude em um triângulo é um segmento perpendicular desenhado de um vértice ao lado oposto. Este lado oposto é chamado de base correspondente à altitude. O comprimento da altitude é a distância entre o topo e a base.

Propriedades das três alturas de um triângulo

As três alturas de um triângulo passam pelo mesmo ponto. Esse ponto é chamado de ortocentro do triângulo .

Você só precisa calcular os componentes desconhecidos nas fórmulas acima para calcular a altura de um triângulo para poder calcular a altura de um triângulo.

• Qual é o foco? Fórmula para calcular o centroide de um triângulo