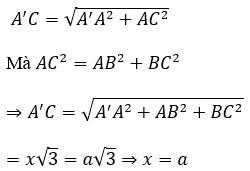Um prisma é um polígono com duas bases paralelas e iguais e faces laterais em forma de paralelogramo.
Comentário:
- As faces laterais de um prisma são iguais e paralelas entre si.
- As faces laterais são paralelogramos.
- As duas bases de um prisma são dois polígonos iguais.
Qual é a fórmula para calcular o volume de um prisma (prisma em V) e qual é a fórmula para calcular o volume de um prisma vertical? Consulte o artigo abaixo.
Índice
1. Volume de um prisma vertical
Fórmula para calcular o volume de um prisma vertical:
O volume de um prisma reto é igual ao produto da área da base multiplicado pela altura.
Lá dentro
Vé o volume do prisma (unidade m3)Bé a área da base (unidade m2)hé a altura do prisma (unidade m)
3. Classificação dos prismas
Prisma regular
É um prisma vertical com uma base poligonal regular. As faces laterais do prisma são todas retângulos iguais. Por exemplo: prisma triangular regular, quadrilátero regular... então entendemos como prisma regular.
Uma base de quadrilátero regular é chamada de prisma de quadrilátero regular.
Prisma triangular
- Um prisma triangular tem 5 faces, 9 arestas e 6 vértices.
- As duas bases são triangulares e paralelas entre si; Cada face lateral é um retângulo;
- Os lados são iguais;
- A altura de um prisma triangular é o comprimento de um lado.
Por exemplo:
O prisma triangular ABC.A'B'C' tem:
- A base inferior é o triângulo ABC, a base superior é o triângulo A'B'C';
As faces laterais são retângulos: AA'B'B, BB'C'C, CC'A'A;
- Bordas:
- Arestas de base: AB, BC, CA, A'B', B'C', C'A'
- Lados: AA', BB', CC';
- Vértices: A, B, C, A', B', C'.
- Altura é o comprimento de um lado: AA' ou BB' ou CC'.
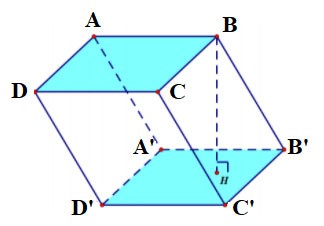
Prisma quadrilátero
- Um prisma quadrilátero tem 6 faces, 12 arestas e 8 vértices.
- As duas bases são quadriláteras e paralelas entre si. Cada face lateral é um retângulo.
- Os lados são iguais.
- A altura de um prisma quadrilátero é o comprimento de um lado.
Por exemplo:
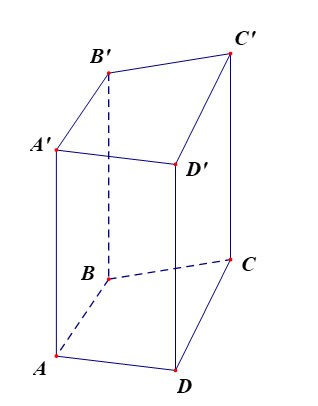
O prisma quadrilátero ABCD.A'B'C'D' tem:
- A base inferior é o quadrilátero ABCD, a base superior é o quadrilátero A'B'C'D';
As faces laterais são retângulos: AA'B'B, BB'C'C, CC'D'D, DD'A'A;
- Bordas:
+ Arestas de base: AB, BC, CD, DA, A'B', B'C', C'D', D'A'
+ Bordas laterais: AA', BB', CC', DD' são iguais.
- Vértices: A, B, C, D, A', B', C', D'.
- Altura é o comprimento de um lado: AA' ou BB' ou CC' ou DD'.
Nota: Prismas retangulares e cubos também são prismas quadriláteros.
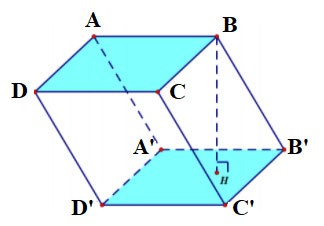
Prisma direito
Se um prisma tem arestas laterais perpendiculares à base, ele é chamado de prisma reto.
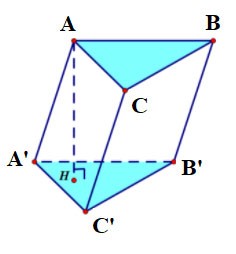
Observação:
Se a base for um retângulo, o cilindro vertical do quadrilátero é chamado de caixa retangular.
Se um cilindro quadrilátero tem 12 lados de comprimento a, então seu nome é cubo.
Compare o prisma direito e o prisma regular:
| DEFINIR: |
NATUREZA |
| + Um prisma vertical é um prisma com um lado perpendicular à base. |
+ As faces laterais de um prisma vertical são retangulares.
+ As faces laterais do prisma são perpendiculares à face da base.
+ Altura é o lado
|
| + Um prisma regular é um prisma vertical cuja base é um polígono regular. |
+ As faces laterais de um prisma são todas retângulos iguais.
+ Altura é o lado
|
4. Exemplo de cálculo do volume de um prisma vertical
Exemplo 1:
Dado o prisma ABC.A'B'C' com base ABC sendo um triângulo equilátero com lado a = 2 cm e altura h = 3 cm. Calcule o volume deste prisma?
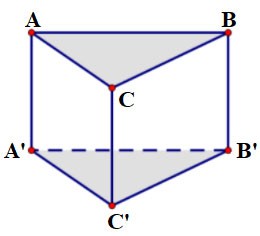
Prêmio:
Como a base é um triângulo equilátero de lado a, a área é:
Neste momento, o volume do prisma é:
Exemplo 2:
Exercício 1: Dada uma caixa vertical com arestas AB = 3a, AD = 2a, AA'= 2a. Calcule o volume do bloco A'.ACD'
Instruir:
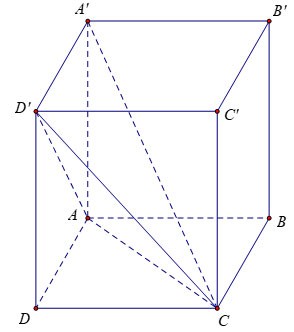
Como a face lateral ADD'A' é um retângulo, temos:
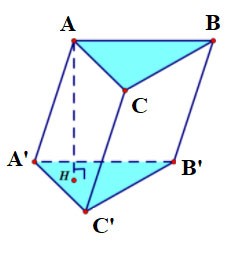
Exemplo 3 : Dado um prisma vertical ABC.A'B'C' cuja base é um triângulo equilátero de lado a√3, o ângulo entre a base e o prisma é 60º. Seja M o ponto médio de BB'. Calcule o volume da pirâmide M.A'B'C'.
Prêmio:
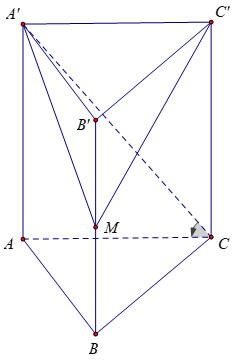
Portanto, podemos inferir que
Nós temos:
Exemplo 4:
Dado um prisma quadrilátero regular ABCD.A'B'C'D' com uma aresta de base de comprimento a e uma face (DBC') formando um ângulo de 60º com a base ABCD. Calcule o volume do prisma ABCD.A'B'C'D?
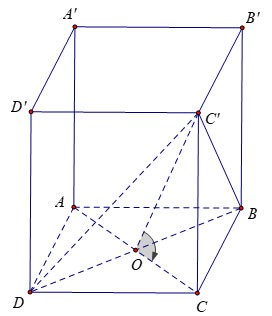
Temos: no centro O do quadrado ABCD.
Por outro lado, portanto,
Inferir
Também:
Exemplo 5:
Calcule o volume V do cubo ABCD.A'B'C'D', sabendo AC'=a√3
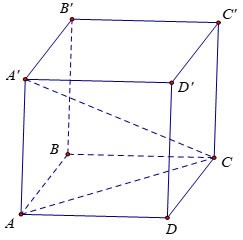
Prêmio:
Seja x o comprimento do lado do cubo.
Considere o triângulo AA'C retângulo em A com:
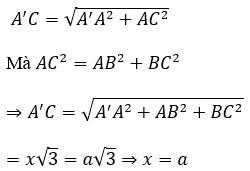
Portanto, o volume do cubo é V=a^3.
Além da fórmula para calcular o volume de um prisma acima, você pode consultar mais artigos sobre a fórmula para calcular o volume de um sólido de revolução , a fórmula para calcular a área e a circunferência de um círculo ...